Surface Water-Groundwater Interaction

1. Introduction

Normally, the response of groundwater to periodic forcing is described in terms of the aquifer head response. It is usual to visualise these results by plotting the spatial distributions of the steady state heads, head amplitudes and head phases (e.g. Colville and Holmes, 1972; Townley, 1995). In two-dimensional simulations, this would result in three separate contour plots to provide an impression of the water table dynamics, but not aquifer flows. The application of Darcy's Law to the nodal head values yields element velocities that are also sinusoidal and characterised by steady and harmonic components. One approach to visualising flow is to compute the total head distribution at selected times throughout a period and display these results in a series of instantaneous equipotentials on which flow vectors (arrows) are drawn. In combining the steady and fluctuating components, however, the potential to explore them individually is lost.

The approach taken in this research is to visualise the steady and harmonic velocity components independently; in the first instance using a conventional flow net approach, and in the case of harmonic flow by introducing the concept of a displacement ellipse. Spatial plots of ellipses provide an intuitive impression of fluid trajectories in purely harmonic velocity fields. The full periodic response of the system, due to the combined effect of steady and harmonic behaviours, is visualised using particle tracking to produce pathlines and streaklines. Because time-harmonic conditions are assumed, transients are identical in each cycle and only one cycle of behaviour need be determined to obtain the response over an arbitrary number of cycles. In an analysis of seasonal variation, this is equivalent to assuming all years are identical. Once the response over one period is known, long-term pathlines are conveniently computed without the need for long simulation times.

2. Velocity Ellipse

Graphical representation of a periodic velocity (single frequency) is achieved by plotting the x-velocity component v_x = x_xs + Re{v_xp exp(i w t)} against the z-velocity component v_z = x_zs + Re{v_zp exp(i w t)} over the period of oscillation P (Figure 1a).

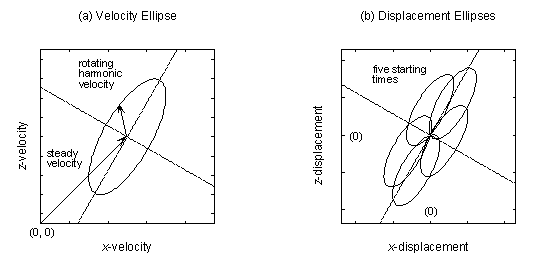Figure 1 - Velocity and displacement ellipses in harmonic flow

The resulting parametric curve is an ellipse with centre located at the point (v_xs, v_zs) and principal axes rotated relative to the x-z-coordinate axes. It is defined in this research as the velocity ellipse. Such Lissajous Figures or Bowditch Curves are well-known in electronics and the study of waves. The shape and rotation of the velocity ellipse is controlled by the ratio of the component amplitudes v_xa / v_za and the phase lag, defined v_lag = arg(v_xp / v_zp).

Though a velocity ellipse has not previously been defined in the context of groundwater studies, Meyboom (1966, Fig.7, p.56) describes a "gradient loop" obtained by plotting the horizontal hydraulic gradient against the vertical gradient at a given location. Plotted field data show a curve that is close to elliptical and reflect strong seasonal forcing in the lake-aquifer system being studied. A similar graphical representation of horizontal tidal currents is used in the study of ocean dynamics (Foreman and Henry, 1989).

Temporarily neglecting the steady component of velocity, the Cartesian equation for an inclined ellipse with centre at the origin (0, 0) is

where the coefficients are functions of the component amplitudes and phases

, ,

The angle of rotation (g) and slopes (m₁ and m₂) of the principal axes are

, ,

When the steady component of velocity is reintroduced, the ellipse is translated by v_xs in the x-direction and v_zs in the z-direction. The principal axes are the lines passing through the point (v_xs, v_zs) with slopes m₁ and m₂.

3. Displacement Ellipse

An important attribute of the velocity ellipse is its usefulness as a visualisation tool. Advective particle trajectories in a uniform, harmonic velocity field (i.e. when the steady flow is neglected) are identical in shape and orientation to the velocity ellipse. The trajectory of a fluid particle is simply the velocity ellipse transformed in dimension by the scale factor 1 / w [T]. Since an ellipse is defined for each point in space, a flow domain can be visualised by 'sampling' the velocity field (e.g. over a regularly spaced grid) and plotting displacement ellipses at each of the sampled point (Figure 2).

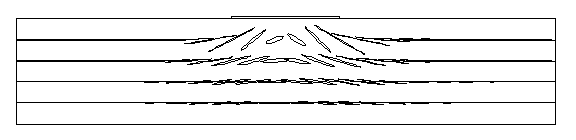Figure 2 - Displacement ellipses beneath a lake with harmonic fluctuation in aquifer recharge

4. Pathlines

Numerical models produce velocity fields that are discrete in space and time. Particle tracking schemes that use this output attempt to compute continuous pathlines by integrating velocity (with respect to time) to estimate displacement. Interpolation schemes are employed to obtain a continuous spatial and temporal distribution of velocity.

The AQUIFEM-P code produces velocities that are spatially discrete across a domain, but continuous sinusoidal functions of time within each element. Pathlines can be computed analytically by integrating the sinusoidal velocities to obtain an analytical expression for displacement. Given the entrance point of a particle on the boundary of an element, and the starting time, the unique exit location and corresponding travel time can be computed exactly. Pathlines can be determined by traversing the domain and searching for entrance and exit locations, element by element. The problem of velocity change during time steps, which arise when velocity is a function of discrete time are avoided.

In a periodic and spatial-uniform velocity field, three basic pathline shapes are possible (Figure 3).

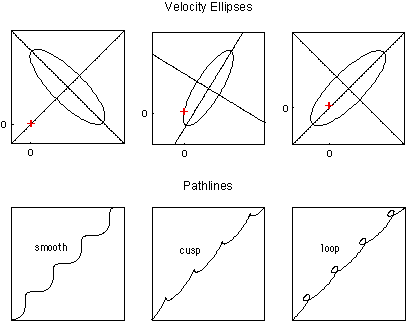Figure 3 - Types of pathlines in periodic flow

The pathline shape can be identified from the velocity ellipse and its position relative to the plot origin. In the first example in Figure 3, the origin lies outside of the velocity ellipse and the generated pathline is smooth and wavy. In the second example a cusp shaped pathline occurs because the ellipse passes exactly through the origin; cusps on the pathline indicate times at which the velocity is zero and correspond to instantaneous stagnation points. The origin is inside the velocity ellipse in the last example, which results in a loopy pathline. In this case both components of velocity reverse direction at the same time, causing the pathline to double back upon itself. Special situations exists when the steady velocity is zero or very small. If zero, the centre of the velocity ellipse is located at the plot origin and particle tracks are precisely elliptical. Oscillatory flows are expected when the steady velocity is small compared to the amplitude of fluctuation

5. Streaklines and Animation

Perhaps less familiar than the concept of a pathline, is a streakline. A streakline is the line that joins the instantaneous positions of all the fluid particles that, at some previous time, have passed through a single fixed location (e.g. Vallentine, 1967, p.16; Bear, 1972, p.225). An example is the purely advective transport of a conservative tracer that is emitted from a continuous point source; the 'plume' is reduced to a line since there is no dispersion. Streamlines, pathlines and streaklines coincide in steady flow, but differ in transient flow. Whereas a pathline indicates the position of a single particle through time - a time history, a streakline shows the instantaneous positions of many particles originating from a common source.

In this research, streaklines are computed by tracking a sequence of particles released at different starting times from selected source locations within the flow domain. The positions of all the particles at the desired 'snap shot' time are joined together to form the streakline. When a series of these images is viewed in smooth succession in a loop, an animation of the flow is obtained (click here to see examples).

Special care is required in regions of divergent flow, such as near to an internal flow divide, otherwise the streakline resolution can be poor due to a low density of particles. Some special handling is also required for streaklines that are comprised of a number of pieces; this can occur when some of the particles released end up outside of the domain. Finally, the computational effort in calculating streaklines is much more numerically intensive than for pathlines. Each point on a streakline is found from an individual pathline and each streakline is generated as a series in time.

References

Bear J. 1972, Dynamics of fluids in porous media. Dover Publications, New York.

Colville JS. Holmes J.W. 1972. Water table fluctuations under forest and pasture in a Karstic region of Southern Australia. Journal of Hydrology 17, 61-80.

Foreman MGG. Henry R.F. 1989. The harmonic analysis of tidal model time series. Advances in Water Resources 12, 109-120.

Meyboom P. 1966. Unsteady groundwater flow near a willow ring in hummocky moraine. Journal of Hydrology 4, 38-62.

Townley LR. 1995. The response of aquifers to periodic forcing. Advances in Water Resources 18(3), 125-146.

Vallentine HR. 1967. Applied Hydrodynamics (2nd ed.). Butterworths, London.